TIERRA Y TECNOLOGÍA Nº 60 | DOI: https://dx.doi.org/10.21028/mac.2022.11.21 | Autores: †Miquel Àngel Cuevas-Diarte, Laura Bayés-García, Teresa Calvet-Pallas. Dpt. Mineralogia, Petrologia i Geologia Aplicada. Facultat de Ciències de la Terra. Universitat de Barcelona. c/ Martí i Franquès, s/n. 08028 Barcelona. macuevasdiarte@ub.edu
Introducción
Si vamos a hablar de simetría, primero definámosla. ¿Qué entendemos por simetría? El diccionario de la Real Academia Española (RAE) nos dice:
- Correspondencia exacta en forma, tamaño y posición de las partes de un todo.
- Biol. Correspondencia que se puede distinguir, de manera ideal, en el cuerpo de una planta o de un animal respecto a un centro, un eje o un plano, de acuerdo con los cuales se disponen ordenadamente órganos o partes equivalentes.
- Geom. Correspondencia exacta en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un centro, un eje o un plano.
Efectivamente, podríamos precisar un poco más, pero es un buen punto de partida.
De hecho, la palabra simetría, que proviene del término griego symmetros, de sym ‘la misma’ y metros ‘medida’, para muchas personas significa más: proporción, equilibrio, orden, armonía, belleza. Es así de rico y complejo.
La simetría es un concepto fundamental de la ciencia, que se utiliza en Matemáticas, Física, Química, Biología, Cristalografía, etc. Pero no tan solo en ciencia. També es habitual en arquitectura, literatura, música, ornamentación, arte, etc.
En nuestro entorno hay una simetría evidente como es la simetría bilateral de muchos animales y plantas, la simetría de rotación de orden 3, 4, 5, 6…en las plantas, la simetría de orden 2, 3, 4, 6 en los cristales, la simetría hexagonal de los copos de nieve, de los enjambres de abejas, de los ojos de los insectos…la simetría de traslación en muchas ornamentaciones.
Otras simetrías menos abundantes son, por ejemplo, las rotaciones de orden superior a 9 que pueden observarse en algunos objetos ornamentales, torres de edificaciones y de iglesias con rotaciones de orden 7, rosetones de catedrales con rotaciones de orden 12 o 16, o plantas octogonales de edificios o ciudades.
Pero sea cual sea su simetría, un conjunto de objetos regularmente distribuidos en el espacio se puede describir con las leyes de la Cristalografía que se aplican a los sólidos cristalinos.
La simetría en el arte es muy abundante desde los principios de la humanidad. Es verdad que más en la pintura o arte decorativas que en la escultura. En la escultura, si se trata de figuras humanas podemos encontrar la simetría bilateral inherente a nosotros. En el caso de la pintura o de les artes decorativas (pavimentos, dibujos en jarrones, cenefas, etc.) la simetría se reduce a una simetría en dos dimensiones, que fundamentalmente incluye la simetría de reflexión (Figura 1), aunque la traslación y las rotaciones en el mismo plano también pueden ser habituales según los casos.
Del cristal
Un cristal es un sólido ordenado y de este orden se deducen una serie de propiedades. Un cristal es periódico (las unidades que lo componen se distribuyen periódicamente en el espacio), es homogéneo (las propiedades de la materia cristalina son idénticas en cada una de sus partes), es anisótropo (las propiedades de la materia cristalina varían con la dirección, como consecuencia de que la periodicidad en el cristal no tiene porqué ser igual a lo largo de todas las direcciones), i es simétrico (las unidades se distribuyen en el espacio siguiendo unos patrones con un cierto contenido de simetría, que hace equivalentes átomos, iones, o moléculas en el cristal).
El estudio o la descripción de un cristal lo podemos abordar a dos niveles: macroscópico y microscópico, los dos estrechamente relacionados. El orden de los átomos, iones o moléculas en el interior del cristal es la causa de que los cristales formen poliedros regulares más o menos bien formados a escala macroscópica. Dicho de otra manera, las formas externas de los cristales son el efecto de su orden interno. La simetría macroscópica es una simetría finita, ya que los poliedros cristalinos son figuras finitas, y el número de operaciones de simetría que los describen también es finito. En cambio, la simetría microscópica es infinita ya que la distribución de átomos, iones o moléculas en el interior del cristal se puede considerar infinita, aunque limitada por las caras. El interior del cristal se describe a la escala del Angstrom. Recordemos que un metro son 1010 Å, es decir, diez mil millones de Angstroms.
Vayamos por partes. Cuando miramos un cristal nos sorprende, de forma inmediata, la existencia de caras planas, formando ángulos precisos, de aristas bien definidas. Sea cual sea el tamaño del cristal. Unas veces las veremos a simple vista y otras será necesaria una lupa, un microscopio óptico, o incluso un microscopio electrónico. Los cristales forman poliedros regulares, como hemos dicho, debido al orden interno de sus componentes. Este orden periódico comporta propiedades que han sido fundamentales para nuestra vida cotidiana. Observando estas morfologías, algunas veces espectacularmente bellas y perfectas, nace la Cristalografía. De hecho, el término cristal proviene de la palabra krystallos con la que los griegos denominaban al hielo y a aquellos minerales transparentes, como el cristal de roca, que suponían formado a partir del frío. Sin entrar en la historia de la Cristalografía, es justo rendir un homenaje a todas aquellas personas que han hecho posible su desarrollo. Inicialmente, y hasta el año 1912 en el que se descubre la difracción de rayos X, que supuso la posibilidad de determinar la estructura interna de los cristales, a partir de su observación macroscópica y de algunas pocas propiedades medibles con instrumentos rudimentarios, tan solo se podían establecer una serie de hipótesis sobre su interior, aunque muchas de ellas corroboradas posteriormente. Fue necesario reinventar la noción de átomo, y después introducir la de molécula, para poder comenzar a introducir la noción de que en el interior del cristal hay una pequeña parte que se repite periódicamente en las tres direcciones del espacio y que nos describe el conjunto del cristal. Este ordenamiento interno se traduce en la morfología que observamos macroscópicamente. Una substancia cristalina tiene una estructura interna determinada y ésta se traduce en una forma externa acorde con ella.
La simetría externa de los cristales, durante mucho tiempo, permitió su clasificación, sobre todo en momentos en que las colecciones de animales, plantas, fósiles y minerales se convirtieron en una moda entre la aristocracia, la burguesía, y los eclesiásticos.
El desarrollo de la Cristalografía ha sido tan espectacular como provechoso para otras ciencias afines, y sus aplicaciones están tan presentes en nuestra vida cotidiana y son de una importancia tan relevante para el progreso de la sociedad del bienestar, que la Asamblea General de las Naciones Unidas declaró 2014 como Año Internacional de la Cristalografía en su reconocimiento.
La forma simétrica de los cristales no deja de ser sorprendente. Es cierto que esta simetría en algunos casos es diferente de la simetría que nos muestran las flores y los animales, o la simetría en algunas obras de arte, de arquitectura, musicales, etc. Pero no menos bella. La complejidad de los seres vivos comporta una libertad de variaciones que en los cristales, donde domina la línea recta, no existe. Pero si las formas cristalinas pueden considerarse esencialmente primitivas desde un punto de vista artístico, poseen, sin duda, una atracción estética. Sus formas nos acercan a la comprensión de su interior y del mundo que nos rodea. La línea recta es un camino que ayuda a la repetición exacta y periódica de una misma unidad, que como hemos dicho es consustancial al cristal. Aunque existen formas cristalinas que podríamos catalogar como “sencillas” como un cubo, muchos cristales, durante su proceso de crecimiento, desarrollan una cantidad y diversidad de caras en la misma forma que incrementan la fascinante complejidad de la forma. Por ejemplo, un cubo puede presentar caras más o menos desarrolladas de octaedro en sus vértices, y de dodecaedro en sus aristas, todas ellas formas de una misma simetría cúbica. Cuando un cristal presenta muchas caras, algunas veces resulta difícil decidir cuáles de ellas deben tomarse como esencialmente del mismo tipo y cuáles corresponderían a formas diferentes. Este ha sido uno de los problemas de los primeros cristalógrafos. Diferentes cristales de una misma sustancia, incluso crecidos al mismo tiempo, normalmente no muestran exactamente la misma forma debido a cambios durante el proceso de crecimiento. Pero los ángulos diedros entre las caras de una misma especie siempre son absolutamente idénticos. Esta fue la base en los albores de esta ciencia. La diversidad de formas cristalinas es extraordinaria. Sin duda es una sinfonía de bellas formas.
La forma externa de los cristales depende de la velocidad relativa de crecimiento de las diferentes caras. Aquellas que tienen una velocidad de crecimiento más baja serán las que tenderán a predominar en la forma cristalina. Las de velocidades elevadas tienden a desaparecer. Las velocidades de crecimiento de las caras, a su vez, dependen de la distribución espacial de las unidades de crecimiento en el interior del cristal. Esta distribución es una consecuencia de las fuerzas de atracción y de la distribución de las fuerzas de enlace entre las unidades estructurales en cada cara. La forma externa del cristal no deja de ser una buena indicación de la distribución simétrica de las unidades estructurales en su interior.
Dicho esto, cuando observamos un cristal que durante el proceso de crecimiento haya desarrollado suficientemente sus caras, lo que podemos apreciar es que algunas de estas caras, son exactamente idénticas las unas a las otras después de efectuar algunos movimientos en el espacio. Es lo que denominamos una operación de simetría. Imaginemos un cubo. Cada cara del cubo es idéntica a otra si la giramos 90º. Y si continuamos girando la cara, después de efectuar cuatro veces el mismo movimiento, reencontramos la cara inicial. Cierto, en el cubo existen rotaciones que nos hacen equivalentes las caras entre sí. De 90º, pero también de 120º si nos situamos en sus vértices, donde veremos tres caras equivalentes. Así mismo podemos dividir las caras en dos mitades con planos paralelos a las aristas, y con planos diagonales de las caras. Todos estos movimientos que dejan invariantes las caras, las aristas o los vértices, son operaciones de simetría macroscópica, y los denominamos elementos de simetría puntual. Y todos los elementos, que en número finito, describen la simetría de un poliedro cristalino se intersectan en un punto que es el centro del poliedro. Por esta razón hablamos de simetría finita en este caso.
Cada poliedro tiene unos elementos de simetría característicos que lo describen y que permiten su clasificación. El conjunto de elementos de simetría de un poliedro forman un grupo de operaciones en el sentido matemático del término. Las matemáticas siempre han sido y son un indispensable soporte a las otras ciencias. De las numerosas combinaciones teóricamente posibles, muchas no son factibles geométricamente en el espacio, y otras dan lugar a combinaciones equivalentes entre sí. En total existen 32 grupos de operaciones de simetría finita o puntual, que se pueden dividir en los 7 sistemas cristalinos.
Las operaciones de simetría son pocas:
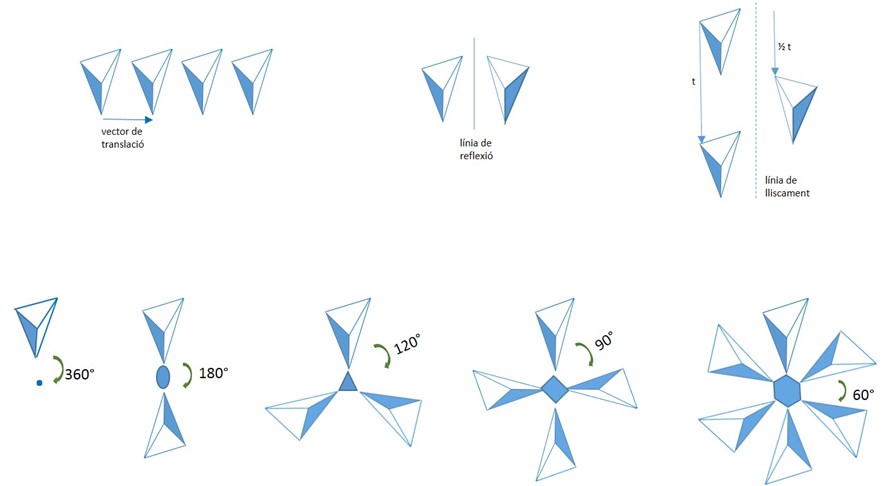
Traslación: Repetición periódica de un objeto en una determinada dirección. Los objetos están separados un cierto vector de traslación con un cierto módulo. Esta operación existe en todas las ornamentaciones infinitas, papeles pintados, mosaicos, interior de un cristal, etc. No está presente cuando se trata de un objeto finito, como un polígono o un poliedro.
Reflexión: Repetición de un objeto por un plano (plano de reflexión o plano de simetría y en dos dimensiones línea de reflexión), de manera que los dos objetos se encuentran equidistantes del plano. Un espejo es un plano de reflexión que nos restituye nuestra imagen reflejada. Los seres vivos superiores estamos divididos por un plano de reflexión (simetría bilateral).
Deslizamiento: Repetición de un objeto por traslación, pero esta vez asociada a una reflexión a media traslación, dando como resultado objetos capiculados a lo largo de una dirección (plano de deslizamiento en tres dimensiones; línea de deslizamiento en dos dimensiones). Como la traslación esta operación está presente en las representaciones periódicas en dos y tres dimensiones. En este último caso, los módulos de los vectores de traslación pueden ser muy diversos.
Rotación: Repetición de un objeto por giro alrededor de un eje (eje de rotación o eje de simetría en tres dimensiones; punto de rotación en dos dimensiones) de un ángulo de 360°/n donde n es el orden del eje. Si n=2 la rotación es de 360/2=180°, si n=3 la rotación es de 360/3=120°, etc. La rotación se produce girando el objeto en el plano perpendicular al eje. Este ángulo puede tomar cualquier valor en los animales, plantas, flores, moléculas aisladas, etc. En los cristales no existen las rotaciones de orden 5, o superiores a 6. En tres dimensiones puede estar asociada a una traslación a lo largo del eje dando lugar a lo ejes helicoidales, que encontramos también en las escaleras de caracol, tornillos de ferretería, etc.
Inversión:Repetición de un objeto respecto de un punto (centro de inversión o centro de simetría) en el espacio. Tan solo existe en tres dimensiones. Algunos objetos contienen el centro de inversión, como un cubo donde los vértices y las aristas están invertidos respecto del punto central del poliedro.
Rotación-Inversión: Repetición de un objeto por giro de un cierto ángulo alrededor de un eje seguido de la inversión respecto del centro de inversión (eje de rotación inversión o eje de inversión). Se trata de una única operación que resulta de la combinación de la rotación y la inversión. Es tan sólo posible en tres dimensiones. Presente, por ejemplo en los poliedros.
La forma externa de un cristal refleja la simetría del grupo puntual de operaciones de simetría. Los cristales están formados por una o varias formas cristalinas, todas ellas correspondientes al grupo puntual del cristal. Una forma cristalina es el conjunto de caras relacionadas entre ellas por la simetría del grupo puntual. Las formas cristalinas pueden ser: sencilla (formada por una sola forma cristalina) o compuesta (formada por más de una forma cristalina). Un octaedro es una forma sencilla. Una forma compuesta estaría formada al mismo tiempo por caras de prisma, de pirámide, etc. Sea una forma sencilla o compuesta, la estructura interna del cristal induce un hábito característico de la morfología externa cristalina. Las unidades estructurales del cristal pueden estar distribuidas de forma similar en las tres direcciones del espacio (hábito isométrico), estar distribuidas predominantemente de forma bidimensional (hábito laminar), tener una dimensión más desarrollada que las otras dos (hábito prismático), o estar distribuidas prácticamente en una dimensión (hábito acicular).
Además, durante el proceso de crecimiento (en la naturaleza o en el laboratorio), los cristales pueden dar lugar a maclas, que son asociaciones de cristales siguiendo una cierta ley de simetría. Como la macla de contacto de la albita, la macla de rotación de la ortoclasa, la macla de interpenetración de la fluorita, la macla cíclica del aragonito, etc.
Si ahora nos situamos en el interior del cristal, ¿qué observaremos? Obviamente átomos, iones o moléculas, según la naturaleza química de la sustancia que estudiemos. En este tránsito recordemos que nos situamos, como ya hemos dicho antes, a la escala del Angstrom. Aquí no nos sirven las lupas, ni los microscopios ópticos. Necesitamos recurrir a la difracción de rayos X (de laboratorio o en un sincrotrón), de neutrones, o de electrones. El orden interno de los cristales comporta que los electrones de los átomos difundan el haz de estas radiaciones en todas las direcciones del espacio y las desvíen en determinadas direcciones con máxima intensidad. A partir del análisis de estas direcciones discretas y de la intensidad en cada una de ellas, somos capaces de determinar dónde están situados los átomos en el espacio tridimensional. Y con mucha precisión, si el cristal es de suficiente calidad y cumple con algunas condiciones.
Este orden interno, microscópico, comporta un cierto contenido de simetría. Aquí hablaremos de simetría microscópica, de simetría espacial, de simetría infinita. Dada la escala a la que nos situamos, el cristal puede considerarse como un universo infinito, limitado per las caras. Las operaciones de simetría hacen equivalentes átomos, iones o moléculas. Son las mismas operaciones que hemos descrito en la simetría macroscópica, y algunas más: la traslación, que asociada a la reflexión da lugar a los planos de deslizamiento, y asociada a la rotación a los ejes helicoidales. También aquí el conjunto de elementos de simetría que describen el interior de un cristal forman un grupo de operaciones en el sentido matemático del término. En dos dimensiones son 17. Es la simetría presente en cualquier dibujo u ornamentación que pretenda llenar todo el plano a partir de un motivo repetido periódicamente por dos translaciones (la mayor parte de papeles pintados que decoran las paredes de las habitaciones, la ornamentación de las paredes y pavimentos en la arquitectura mudéjar de Aragón o de la Alhambra de Granada, o de Los Reales Alcázares de Sevilla, los pavimentos de muchas aceras de nuestras ciudades). En tres dimensiones son 230 los grupos de operaciones de simetría espacial o de simetría infinita. Si introducimos diferencias de color (simetría policromática) los grupos aumentan a 1651 en simetría dicromática. Cada uno de estos grupos de operaciones de simetría espacial es el resultado de combinar una red de puntos, que representa la distribución periódica de los átomos, iones o moléculas en el interior del cristal, con el conjunto de operaciones de simetría que representan las equivalencias entre los átomos, iones o moléculas en el espacio. En dos dimensiones consideramos cinco redes planas en función de la simetría que pueden contener, y en tres dimensiones son 14. En todos los casos la geometría de la red queda configurada por la simetría que incluye.
Y mucho más
Como dicen muchos autores, y entre ellos Coxeter (1969), algunas de las operaciones de simetría que hemos definido en el cristal pueden visualizarse también en muy diversos lugares y situaciones. Por citar tan solo un ejemplo sencillo, en las letras mayúsculas. Entre otras, la E contiene una reflexión horizontal, la A una vertical, la N una rotación de 180°, y la H dos reflexiones perpendiculares con una rotación binaria en su intersección, tal como muestra la Figura 2.
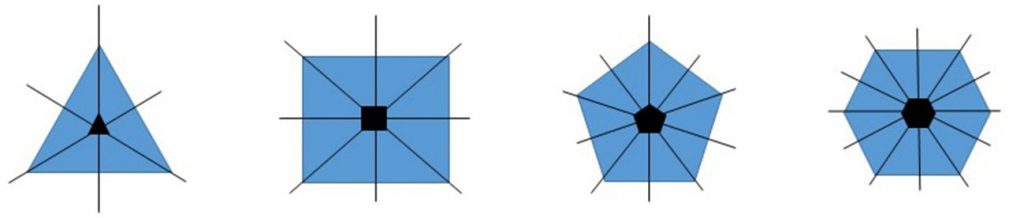
Igualmente las podemos observar en los polígonos. Un triángulo contiene tres reflexiones y un punto de rotación de orden 3 en su intersección, un cuadrado cuatro con un punto de rotación de orden 4, un pentágono cinco con la rotación de orden 5, un hexágono seis…como muestra la Figura 3.
Inicialmente, el arte pictórico y escultórico ha sido, sobre todo, una imitación de la naturaleza. De hecho, antes de incorporar los diferentes tipos de perspectiva y otros elementos, a menudo la simetría se impone a la imitación de la naturaleza. Otras veces la representación no es tan simétrica como parece a primera vista. Pero incluso en representaciones asimétricas podemos ver la simetría como norma de la cual nos alejamos. La simetría bilateral se diluye cada vez más en una noción vaga de dibujo equilibrado como puede apreciarse en la Figura 4. No obstante, una de las simetrías más frecuentes en la pintura es la reflexión (Cuevas-Diarte 2015).

Dando un gran salto en el tiempo Salvador Dalí (1904-1989), artista genial, gran interesado en la ciencia y en abrir nuevos caminos en el arte, basaba parte de su obra en los principales fundamentos teóricos del Discurso sobre la figura cúbica de Juan de Herrera, geómetra, matemático y arquitecto, quien, a su vez, había elaborado su Discurso bajo la inspiración de estudios sobre geometría de Ramón Llull, que en la época medieval proponía vincular la ciencia y la religión con el conocimiento. En A propósito del “Discurso sobre la forma cúbica” de Juan de Herrera, como ya había hecho anteriormente en obras como Corpus hipercubus el artista se basa en las teorías herrerianas sobre los principios de la formación del cubo. Dalí propone la imagen de un cubo insertado en otra forma cúbica (un hipercubo) construida a partir de letras, que se pueden leer en diversas direcciones, y con el nombre del arquitecto (Juan) en sus aristas.

En la ornamentación, la traslación y la reflexión (aislada o combinada con la traslación en un deslizamiento) están frecuentemente presentes. La Figura 6 muestra un modelo.

Los mosaicos y pavimentos son otro ejemplo. Desde la antigüedad, y en particular durante las civilizaciones griega y romana, los mosaicos han constituido un elemento ornamental importante, y en ello observamos una cierta simetría, como no puede ser de otra manera. Los papeles pintados, las alfombras, y muchos otros elementos muestran simetría. En la actualidad también, algunas obras de artistas famosos como Ai WeiWei también se basan en la simetría (Figura 7).
Y los pavimentos de muchas casas, no exclusivamente modernistas, que también, y de las calles nos muestran diferentes tipos de simetría: hexagonal como en las baldosas Gaudí del paseo de Gracia de Barcelona (Figura 8), cuadrada en las baldosas Barcelona de otras calles de la ciudad. Cuando “llenamos” un plano, sea el suelo, una pared, un techo… con un cierto motivo que se repite periódicamente, introducimos simetría. Es obligado.
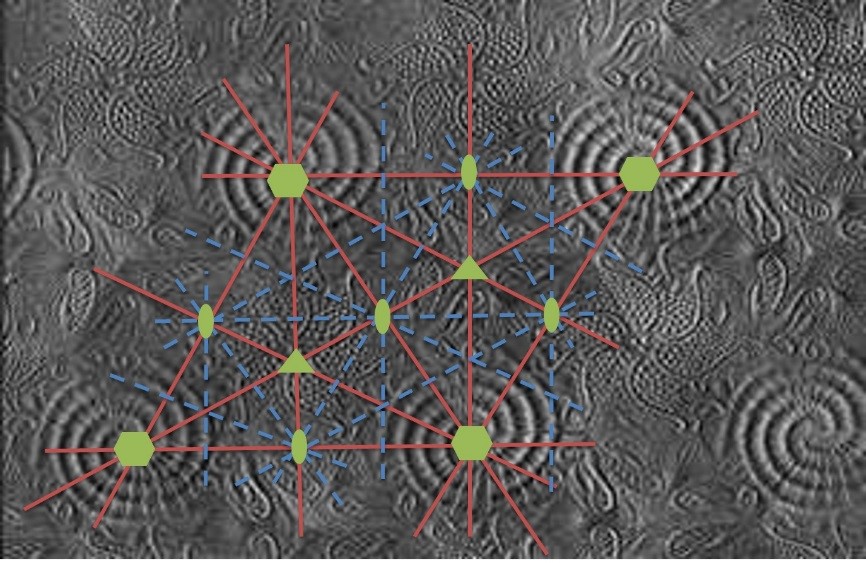
Estos pavimentos, papeles pintados, etc. podemos considerar que se han generado a partir de la repetición periódica de un “motivo” en las dos direcciones del plano por dos vectores de traslación no paralelos. Los extremos de estos vectores forman una red o retículo de puntos en el plano. Los dos vectores delimitan un paralelogramo que por repetición en las dos direcciones del plano, generan todo el dibujo. Diferentes valores de los módulos de los dos vectores y del ángulo que forman, generan diversas geometrías del retículo. Sin ánimo de entrar a describirlos, diremos que tan solo hay cinco tipos de redes planas o bidimensionales. Su geometría viene determinada por la simetría que contenga. Si la simetría es baja, los módulos y el ángulo entre los vectores pueden tener cualquier valor. Si la simetría es alta, la geometría queda fijada: por ejemplo, si contiene rotaciones 90°, los dos vectores deberán tener módulos idénticos y el ángulo entre ellos ha de ser de 90° (red cuadrada); si contiene rotaciones de 120° el ángulo ha de ser de 120°. El conjunto de elementos de simetría de una red bidimensional forman un grupo en el sentido matemático del término, y tan solo hay 17. Los diecisiete los podemos encontrar representados en los magníficos ornamentos de la Alhambra de Granada, por ejemplo. El extraordinario artista M. C. Escher los representó a partir de motivos muy diversos y originales, y la Unión Internacional de Cristalografía los adoptó como modelos de ejercicios cristalinos. La Figura 9 muestra un ejemplo de red bidimensional. En tres dimensiones seguiríamos el mismo patrón pero un poco más complicado.
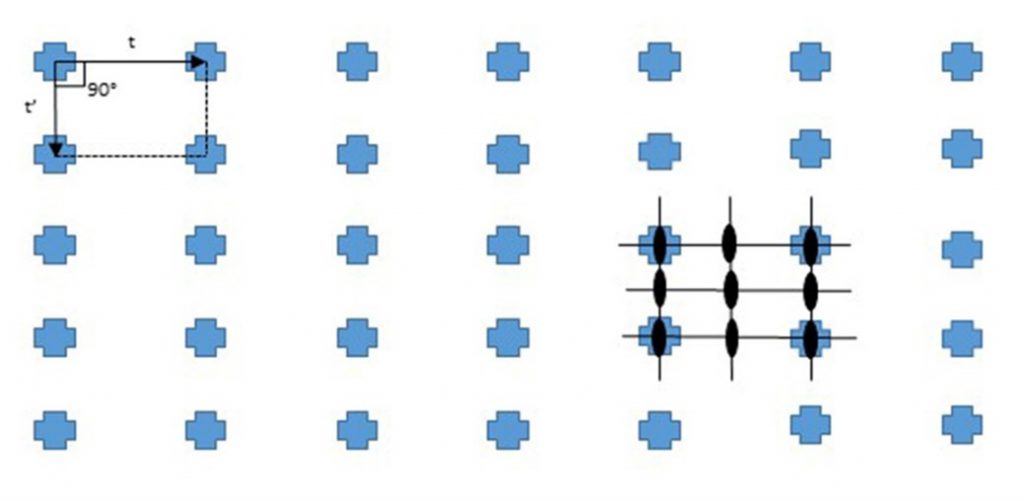
Como se describe en Cuevas-Diarte et al. (2017), este modelo de retículo bidimensional puede aplicarse también al Ensanche de Cerdà que supuso la expansión de Barcelona fuera de sus murallas medievales (Figura 10). Cerdà estructuró la nueva Barcelona en calles perpendiculares entre sí, excepto alguna vía en diagonal o siguiendo un meridiano o un paralelo terrestres, que obedece a un sentido de regularidad, de ciudad equilibrada e igualitaria, que puede crecer en todos los sentidos. Si prescindimos de los detalles de los edificios, el conjunto de “islas” o “manzanas” de casas del Ensanche se repiten periódicamente en las dos direcciones del plano tal como hemos descrito en los pavimentos o en los papeles pintados. Esta repetición periódica comporta una simetría de traslación. Si nos situamos en uno de sus cruces, cualquiera de ellos al azar, que tomaremos como origen de coordenadas, encontramos otro cruce prácticamente idéntico al final de la isla de casas tanto si nos desplazamos por una de las calles o por la calle perpendicular. Hemos definido dos vectores de traslación de módulos prácticamente idénticos y que forman un ángulo de 90º. Estos dos vectores definen una superficie que podemos repetir en las dos direcciones del plano de forma continuada en todo el Ensanche. Es el mismo modelo que utilizamos en la materia cristalina, aunque en este caso el conjunto sería tridimensional. Podemos referirnos a la Figura 9 con la excepción de que en el retículo del ensanche los módulos de los dos vectores son idénticos y el ángulo entre ellos de 90º, ya que la red es una red cuadrada, con simetría de rotación de 180 y de 90º y reflexiones según los lados, a media distancia y según las diagonales del cuadrado que configuran los vectores de traslación.

Siguiendo en el ámbito de la arquitectura y centrados en Barcelona aunque puede hacerse extensible a otras muchas ciudades, la simetría está presente también en muchas de las fachadas de nuestros edificios. En este caso, excepto excepciones, se limita a una simetría de reflexión y/o de traslación. Elementos como las ventanas o los balcones se repiten periódicamente a lo largo de la fachada y en muchos casos están relacionados por líneas verticales de reflexión y alguna vez también horizontales. En edificios más modernos como algunas torres de vidrio, cada uno de ellos puede idealizarse como un prisma tetragonal. Prisma por las cuatro caras paralelas a la dirección vertical. Tetragonal porque verticalmente contiene un eje de rotación de orden 4 que nos hace equivalentes los cuatro lados por una rotación de 90º. También podemos observar ejes de rotación de orden 2 perpendiculares al principal, así como reflexiones verticales a mitad de las caras del prisma y según las diagonales, y una reflexión horizontal que nos divide el edificio en la mitad superior y la mitad inferior. La geometría inducida por esta simetría hace que los dos lados de la torre sean iguales, con una planta cuadrada. Si, por el contrario, la planta es rectangular en lugar de cuadrada, entonces el eje de orden cuatro desaparece y la simetría se reduce a tres ejes de rotación de orden 2 perpendiculares entre sí, con tres planos de reflexión perpendiculares a cada uno de los ejes. Se trata entonces de un prisma rómbico.
Algunos otros elementos de la ciudad también se caracterizan por su simetría. Estamos pensando en las fuentes de agua, en las farolas, de los pavimentos de los cuales ya hemos hablado, así como de muchos elementos de ornamentación que se encuentran en nuestras calles o en el interior o en el exterior de algunos edificios: puertas, apliques de luz, cerámicas, vidrieras, esgrafiados, etc.
Otro ámbito del arte en el que se observa simetría es la escultura. Aquí la simetría se manifiesta habitualmente por su bilateralidad, sobre todo en la antigüedad. Tal como sucedía con la pintura las esculturas eran “planas”, representaban la vista frontal de las personas (ley de la frontalidad). Las figuras se esculpían para ser contempladas de frente, lo que repercute en que sean muy simétricas, con un plano de reflexión vertical muy marcado, que hace que las dos partes sean prácticamente idénticas. Los escultores griegos fueron los primeros en abandonar este convencionalismo. Posteriormente las figuras escultóricas pierden muchas veces esta simetría bilateral, aunque a menudo pueda estar presente, como en la escultura del gato de Fernando Botero (1932- ) que, después de haber vivido en diferentes emplazamientos, se encuentra actualmente en la Rambla del Raval de Barcelona. Otros artistas hacen una interpretación personal, como es el caso de la escultura de Joan Miró (1893-1983) que se encuentra en la entrada de la Fundación Miró de Barcelona, o de Jaume Plensa (1955- ) en su obra que situada al lado del Palau de la Música de Barcelona (Figura 11).

En fotografía la simetría está presente en diversos aspectos. Por una parte, una foto puede mostrar una imagen simétrica en ella misma, como muestra la Figura 12 con una reflexión del paisaje en el agua que nos recuerda algunas pinturas conocidas (históricamente la teoría fotográfica se retroalimenta de las fuentes de la pictórica), o constituir la base de la composición de la foto establecida normalmente a partir de la aplicación de la “regla de los dos tercios” o de la “proporción áurea”.
Un elemento directamente relacionado con la simetría y que es recurrente a lo largo del tiempo en pinturas y esculturas son los poliedros. Los poliedros, en ellos mismos, contienen algunos elementos de simetría: reflexiones, rotaciones, inversiones. Estas operaciones de simetría en el espacio relacionan, hacen equivalentes caras, aristas o vértices. Por ejemplo, en un cubo las caras se repiten cada 90° por rotación alrededor de un eje que idealmente “sale” por el centro de cada una de las caras; o queda dividida por la mitad por unos planos ideales de simetría de reflexión, tanto verticalmente como horizontalmente como según sus diagonales; o son idénticas por inversión en el espacio respecto del punto central del poliedro. Todos los elementos de simetría de un poliedro se cruzan en un punto que es su punto central: por eso hablamos de simetría puntual en este caso. En cada poliedro los elementos de simetría son diferentes, a pesar de que hay grupos que los comparten, y también aquí el conjunto de elementos de simetría de un poliedro forman un grupo en el sentido matemático del término: un total de 32 si consideramos los poliedros cristalográficos. En los poliedros no encontramos la traslación como operación de simetría ya que se trata de una simetría finita que relaciona elementos finitos. Recordemos que un poliedro es un sólido limitado por caras planas. El término poliedro deriva del griego polis “muchas” y hedra “caras”. Un poliedro es un cuerpo geométrico formado por una cantidad finita de polígonos planos. Cada uno de estos polígonos forma una cara, las caras se interceptan en aristas, y las aristas convergen en un vértice. Los poliedros tienen caras, aristas y vértices, mientras que los polígonos tienen lados y esquinas. Podemos considerar que la pirámide (y por añadidura la bipirámide) y el prisma son los poliedros básicos que se repiten y adjetivan según su simetría (prisma rómbico, bipirámide hexagonal, etc.) mientras que otros poliedros toman nombres específicos (dodecaedro, esfenoedro, etc.).
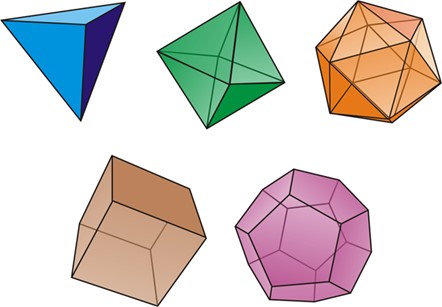
Cinco son los poliedros que por su historia y por su transcendencia, desde la geometría a la filosofía, debemos resaltar. Hablamos de los cinco sólidos platónicos: tetraedro, octaedro, icosaedro, cubo, y dodecaedro. Todos ellos son poliedros regulares: a) Todas las caras son polígonos regulares iguales; b) En todos los vértices se interceptan el mismo número de caras y de aristas; c) Todas las aristas tienen la misma longitud; d) Todos los ángulos diedros son iguales. No hablaremos aquí de otros poliedros también simétricos como los sólidos Arquimedianos, los de Johnson, los de Catalan, etc. (Álvarez (2005) o Cromwell (1997). Los poliedros aparecen al largo de la historia en muy diferentes ámbitos artísticos. En Internet podemos encontrar excelentes recopilaciones como la del profesor Hart. Como dice Philibert “los poliedros han seducido al espíritu humano desde los albores de la humanidad”. A pesar de que los minerales cristalizados habían sido admirados desde siempre, son los griegos los primeros que abordan su estudio y comprensión. Son ellos los que utilizan por primera vez el término cristal para referirse a aquellos minerales con formas poliédricas que por su transparencia creían que era agua congelada. Primero Pitágoras (572 a.C.) y su escuela, basada principalmente en los números, proponen la noción de proporción. La proporción implica que nos referimos a una escala, a un patrón, una dimensión de referencia, como por ejemplo la altura humana. Los pitagóricos consideraban que la base de la armonía eran las proporciones: es bello si posee unas proporciones justas. Después Platón (427-347 a.C.). Para la escuela platónica simetría es sinónimo de armonioso, proporcionado, y al mismo tiempo ordenado. La simetría es, ante todo, una semblanza con las formas inteligibles, las Ideas. Esta semblanza o analogía es lo que permanece constante, invariante, inmutable en el curso de todas las transformaciones. Una propiedad no cambia en el curso del cambio. Es decir, durante el cambio alguna cosa permanece similar. La simetría que definen los platónicos incluye la identidad de dos partes superponibles, pero sobre todo se manifiesta por la constancia de las proporciones. Es un concepto matemático, pero no exclusivamente matemático. Así, la belleza, el orden, la armonía, la proporción, la justicia, todo lo que está hecho con mesura manifiesta la simetría. Platón considera que el Universo ha de estar formado por componentes elementales que posean simetría, y que han de ser tan perfectos como sea posible. Por eso relaciona cuatro poliedros, considerados como los objetos geométricos más perfectos, con los elementos que según su escuela constituyen la materia: la tierra se asoció con el cubo, el aire con el octaedro, el agua con el icosaedro y el fuego con el tetraedro. Esta asociación no parece responder a una clara justificación. El quinto sólido platónico, el dodecaedro, Platón lo asocia con el Universo, pensando que debía tener relación con la sustancia de la que están hechos los planetas y las estrellas (Figura 13).
Habrá que esperar hasta el Renacimiento para encontrar a los sólidos platónicos como objeto de estudio. Tal vez el trabajo más completo puede considerarse realizado hacia 1480 por Piero della Francesca (1415-1492), que escribió un tratado sobre los cinco sólidos. En la misma época, su alumno Luca Pacioli (1445-1517), inspirándose en los trabajos de las escuelas platónica y euclidiana (y en primera instancia pitagórica), en la obra de Vitrubio (70-15 a.C.), en conversaciones con Leonardo da Vinci (1452-1519) y en los trabajos de Piero della Francesca, realiza la construcción y un estudio exhaustivo de los poliedros regulares y semirregulares en la su obra De Divina proportione. Pacioli, basándose en Euclides (325-265 a.C.), incide en la importancia matemática de la sección de oro, la divina proporción como la denomina. Los trabajos de Piero della Francesca y Luca Pacioli sobre poliedros tuvieron una gran incidencia en la posterior literatura matemática vinculada al arte, sobre todo la desarrollada por Durero (1471-1528), que escribe una especie de enciclopedia geométrica para uso de pintores con la que pretende dotar a la creación artística de una base científica-geométrica. Posteriormente, Kepler (1571-1630), seducido por la misma línea de pensamiento, elabora una cosmología basada en los cinco sólidos regulares, en la creencia de que eran la llave para la construcción de la estructura del Universo. Descartes (1596-1650) y Euler (1707-1783) también estudian los poliedros desde el punto de vista matemático. Durante los siglos XVII y XVIII los poliedros son motivo constante de estudio de la mano del desarrollo de diversas ciencias como la Cristalografía y la Mineralogía. A finales del siglo XIX, el estudio de los poliedros recibió un nuevo impulso con la aplicación de la teoría de grupos en Matemáticas y Cristalografía.
Philibert remarca la seducción que los poliedros ejercieron sobre los artistas del Renacimiento. En el Museo de los Ufficci, una pintura de 1495 representa al matemático Luca Pacioli haciendo una demostración de geometría (Figura 14). Se pueden ver dos poliedros: sobre el libro, un dodecaedro pentagonal y, suspendido de un hilo, un objeto translúcido que podría ser identificado como uno de los catorce poliedros de Arquímedes. Vale la pena documentarse sobre algunos de los enigmas que incluye esta pintura. Pacioli, como hemos dicho anteriormente, habla de la proporción divina, un término relativo a la razón o proporción ligada al denominado número áureo. Para Pacioli, la proporción más significativa es la que corresponde al número de oro, 1,618…que se deduce de la proporción entre extremo y mediana de Euclides. Partiendo de un estudio muy riguroso de los trabajos de Euclides, muestra que ciertos sólidos platónicos pueden inscribirse en esferas, y que su construcción geométrica se basa en algunas proporciones entre la cuales el famoso 1,618…Estas proporcione, dichas “divinas” evocan las Ideas de Platón, pero en realidad, para él, conducen a Dios. Puede, así, proponer una síntesis entre las tesis platónicas y la religión cristiana. El libro trata, entre otras cuestiones, de los polígonos, de las ideas arquitectónicas de Vitrubio y de los sólidos platónicos o regulares, y contiene ilustraciones que encargó a Leonardo da Vinci. Para Leonardo, la belleza consiste en la divina proporción que los miembros manifiestan en su conjunto y que muestran como una armonía divina resultado de su acuerdo.

A propósito de la proporción áurea y volviendo un momento a la arquitectura, las pirámides egipcias son un buen ejemplo. Construidas como monumentos funerarios, son perfectas pirámides tetragonales, es decir, su eje principal lo podemos imaginar como un eje de rotación de orden 4 que hace equivalentes las caras cada 90°. Algunos han querido ver en las pirámides, como en los templos griegos y otras construcciones, el número de oro, aunque no hay constancia de que sus arquitectos tuviesen conocimiento de este concepto y lo hubieran tenido en cuenta al planificarlos. A pesar de ello, es verdad que la razón entre la altura de una cara y la mitad del lado de la base de una pirámide es, aproximadamente, 1’618…, es decir, el número de oro, así como el cociente entre el área total y el área lateral de la pirámide, y el cociente entre el área lateral y el área de la base. El número de oro representa una proporción agradable, que implícita o explícitamente es utilizada en situaciones diversas. Todos llevamos encima tarjetas de crédito que obedecen a esta proporción divina.
Como hace notar Amorós (1978), “cuantas veces y cuan numerosas personas se han sentido atraídas por la belleza y la armonía de la forma cristalina. No hay duda de que la regularidad geométrica de un mineral cristalizado, juntamente con su transparencia única, la dureza y a menudo el color, transforma la observación en una experiencia estética. Son precisamente estas cualidades estéticas las que impulsan a coleccionar minerales cristalizados, ya que un cristal es, ante todo, un objeto de extraordinaria belleza. Si los cristales son bellos, no podía ser de otra manera que en el Renacimiento, que produjo una explosión de sentimientos artísticos, al mismo tiempo que se reconocía el valor de la observación directa de la naturaleza, se utilizase por primera vez el cristal como elemento decorativo, y que, como consecuencia, se representase de manera fidedigna. Y no es de extrañar que esta empresa fuese iniciada por el artista y no por el hombre de ciencia”.
La simetría continúa teniendo un papel importante en las ciencias y en las artes, contribuyendo al desarrollo del conocimiento, a partir de la conjunción de las matemáticas, la experimentación, y la Cristalografía moderna.
La simetría se convierte en una noción clave en el conjunto de disciplinas científicas contemporáneas. Si definimos la simetría como la correspondencia por translación, rotación o reflexión en el espacio, podemos constatar que esta acepción se sitúa en el centro de las ciencias de la materia, así como en biología, tanto a escala macroscópica como microscópica. La simetría, incluyendo la quiralidad, nos permite tratar las formas tridimensionales de las moléculas aisladas, los sólidos, la estructura del genoma, etc.
Si inicialmente los griegos hablan de simetría como la proporción entre el todo y las partes, con el paso del tiempo y la influencia de las diferentes disciplinas que se desarrollan, el concepto de simetría se aplica también a la identidad como superposición de dos partes derecha e izquierda de una misma figura, incluyendo actualmente la correspondencia entre las partes de una figura respecto de un plano, un eje, un punto, o algunas de las combinaciones de estos elementos. Además, el término de simetría guarda todavía alguna relación con su sentido inicial, ya que le podemos añadir el calificativo de agradable, de armonía, e incluso de belleza.
Referencias bibliográficas
- Álvarez, S. 2005. Polyhedra in (inorganic) chemistry”. Dalton Transactions 13, 2209-2233.
- Amorós, J.L. 1978. La gran aventura del cristal. Naturaleza y evolución de la ciencia de los cristales. Editorial de la Universidad Complutense de Madrid.
- Coxeter, H. S. M. 1969. Introduction to geometry. Second edition. John Wiley & Son, Inc. New York.
- Cuevas-Diarte, M.A. 2015. Simetria. Un passeig interdisciplinari. Edicions de la Universitat de Barcelona. Barcelona.
- Cuevas-Diarte, M.A., Pesoa Marcilla, M. and Roca Blanch, E. 2017. Simetries de Barcelona. Edicions de la Universitat de Barcelona. Barcelona.
- Cromwell, P.R. 1997. Polyhedra. Cambridge University Press.
- Hart, G.W. Virtual Polyhedra. http://www.georgehart.com/virtual-polyhedra
- Philibert, J. 2010. La symétrie dans la nature, dans la science et dans l’art. http://e-materials.ensiacet.fr/documents/symetrie_philibert.pdf